TensorFlow更新模型变量。它能一次操作一个数据点,也可以一次操作大量数据。一个训练例子上的操作可能导致比较“古怪”的学习过程,但使用大批量的训练会造成计算成本昂贵。到底选用哪种训练类型对机器学习算法的收敛非常关键。
为了TensorFlow计算变量梯度来让反向传播工作,我们必须度量一个或者多个样本的损失。
随机训练会一次随机抽样训练数据和目标数据对完成训练。另外一个可选项是,一次大批量训练取平均损失来进行梯度计算,批量训练大小可以一次上扩到整个数据集。这里将显示如何扩展前面的回归算法的例子——使用随机训练和批量训练。
批量训练和随机训练的不同之处在于它们的优化器方法和收敛。
# 随机训练和批量训练
#----------------------------------
#
# This python function illustrates two different training methods:
# batch and stochastic training. For each model, we will use
# a regression model that predicts one model variable.
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from tensorflow.python.framework import ops
ops.reset_default_graph()
# 随机训练:
# Create graph
sess = tf.Session()
# 声明数据
x_vals = np.random.normal(1, 0.1, 100)
y_vals = np.repeat(10., 100)
x_data = tf.placeholder(shape=[1], dtype=tf.float32)
y_target = tf.placeholder(shape=[1], dtype=tf.float32)
# 声明变量 (one model parameter = A)
A = tf.Variable(tf.random_normal(shape=[1]))
# 增加操作到图
my_output = tf.multiply(x_data, A)
# 增加L2损失函数
loss = tf.square(my_output - y_target)
# 初始化变量
init = tf.global_variables_initializer()
sess.run(init)
# 声明优化器
my_opt = tf.train.GradientDescentOptimizer(0.02)
train_step = my_opt.minimize(loss)
loss_stochastic = []
# 运行迭代
for i in range(100):
rand_index = np.random.choice(100)
rand_x = [x_vals[rand_index]]
rand_y = [y_vals[rand_index]]
sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
if (i+1)%5==0:
print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)))
temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})
print('Loss = ' + str(temp_loss))
loss_stochastic.append(temp_loss)
# 批量训练:
# 重置计算图
ops.reset_default_graph()
sess = tf.Session()
# 声明批量大小
# 批量大小是指通过计算图一次传入多少训练数据
batch_size = 20
# 声明模型的数据、占位符
x_vals = np.random.normal(1, 0.1, 100)
y_vals = np.repeat(10., 100)
x_data = tf.placeholder(shape=[None, 1], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
# 声明变量 (one model parameter = A)
A = tf.Variable(tf.random_normal(shape=[1,1]))
# 增加矩阵乘法操作(矩阵乘法不满足交换律)
my_output = tf.matmul(x_data, A)
# 增加损失函数
# 批量训练时损失函数是每个数据点L2损失的平均值
loss = tf.reduce_mean(tf.square(my_output - y_target))
# 初始化变量
init = tf.global_variables_initializer()
sess.run(init)
# 声明优化器
my_opt = tf.train.GradientDescentOptimizer(0.02)
train_step = my_opt.minimize(loss)
loss_batch = []
# 运行迭代
for i in range(100):
rand_index = np.random.choice(100, size=batch_size)
rand_x = np.transpose([x_vals[rand_index]])
rand_y = np.transpose([y_vals[rand_index]])
sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
if (i+1)%5==0:
print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)))
temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})
print('Loss = ' + str(temp_loss))
loss_batch.append(temp_loss)
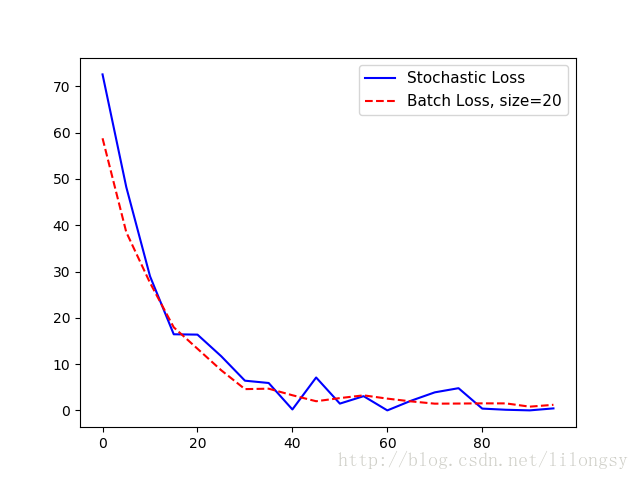
plt.plot(range(0, 100, 5), loss_stochastic, 'b-', label='Stochastic Loss')
plt.plot(range(0, 100, 5), loss_batch, 'r--', label='Batch Loss, size=20')
plt.legend(loc='upper right', prop={'size': 11})
plt.show()
输出:
Step #5 A = [ 1.47604525] Loss = [ 72.55678558] Step #10 A = [ 3.01128507] Loss = [ 48.22986221] Step #15 A = [ 4.27042341] Loss = [ 28.97912598] Step #20 A = [ 5.2984333] Loss = [ 16.44779968] Step #25 A = [ 6.17473984] Loss = [ 16.373312] Step #30 A = [ 6.89866304] Loss = [ 11.71054649] Step #35 A = [ 7.39849901] Loss = [ 6.42773056] Step #40 A = [ 7.84618378] Loss = [ 5.92940331] Step #45 A = [ 8.15709782] Loss = [ 0.2142024] Step #50 A = [ 8.54818344] Loss = [ 7.11651039] Step #55 A = [ 8.82354641] Loss = [ 1.47823763] Step #60 A = [ 9.07896614] Loss = [ 3.08244276] Step #65 A = [ 9.24868107] Loss = [ 0.01143846] Step #70 A = [ 9.36772251] Loss = [ 2.10078788] Step #75 A = [ 9.49171734] Loss = [ 3.90913701] Step #80 A = [ 9.6622715] Loss = [ 4.80727625] Step #85 A = [ 9.73786926] Loss = [ 0.39915398] Step #90 A = [ 9.81853104] Loss = [ 0.14876099] Step #95 A = [ 9.90371323] Loss = [ 0.01657014] Step #100 A = [ 9.86669159] Loss = [ 0.444787] Step #5 A = [[ 2.34371352]] Loss = 58.766 Step #10 A = [[ 3.74766445]] Loss = 38.4875 Step #15 A = [[ 4.88928795]] Loss = 27.5632 Step #20 A = [[ 5.82038736]] Loss = 17.9523 Step #25 A = [[ 6.58999157]] Loss = 13.3245 Step #30 A = [[ 7.20851326]] Loss = 8.68099 Step #35 A = [[ 7.71694899]] Loss = 4.60659 Step #40 A = [[ 8.1296711]] Loss = 4.70107 Step #45 A = [[ 8.47107315]] Loss = 3.28318 Step #50 A = [[ 8.74283409]] Loss = 1.99057 Step #55 A = [[ 8.98811722]] Loss = 2.66906 Step #60 A = [[ 9.18062305]] Loss = 3.26207 Step #65 A = [[ 9.31655025]] Loss = 2.55459 Step #70 A = [[ 9.43130589]] Loss = 1.95839 Step #75 A = [[ 9.55670166]] Loss = 1.46504 Step #80 A = [[ 9.6354847]] Loss = 1.49021 Step #85 A = [[ 9.73470974]] Loss = 1.53289 Step #90 A = [[ 9.77956581]] Loss = 1.52173 Step #95 A = [[ 9.83666706]] Loss = 0.819207 Step #100 A = [[ 9.85569191]] Loss = 1.2197
| 训练类型 | 优点 | 缺点 |
|---|---|---|
| 随机训练 | 脱离局部最小 | 一般需更多次迭代才收敛 |
| 批量训练 | 快速得到最小损失 | 耗费更多计算资源 |
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持脚本之家。